Diagram Venn: Difference between revisions
No edit summary |
|||
| (7 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
Kalian bisa menulis adanya sebuah himpunan dengan menggunakan tanda kurung, seperti: | Kalian bisa menulis adanya sebuah himpunan dengan menggunakan tanda kurung, seperti: | ||
{topi, baju, jaket, celana,…} | {topi, baju, jaket, celana,…} | ||
Atau kalian juga bisa menulis himpunan di dalam sebuah bilangan, seperti: | Atau kalian juga bisa menulis himpunan di dalam sebuah bilangan, seperti: | ||
Himpunan seluruh bilangan : {0,1,2,3…} | Himpunan seluruh bilangan : {0,1,2,3…} | ||
Himpunan bilangan prima: {2,3,5,7,11,13,…} | Himpunan bilangan prima: {2,3,5,7,11,13,…} | ||
Diagram venn yang di dalamnya berisi suatu himpunan tadi digambarkan dengan bentuk diagram sehingga mudah untuk dipahami. | Diagram venn yang di dalamnya berisi suatu himpunan tadi digambarkan dengan bentuk diagram sehingga mudah untuk dipahami. | ||
Untuk cara menggambarnya, kalian dapat memperhatikan gambar di bawah ini. | Untuk cara menggambarnya, kalian dapat memperhatikan gambar di bawah ini. | ||
[[File:Diagramvenn01.jpg|thumb|center|300px]] | |||
'''Keterangan Gambar''' | '''Keterangan Gambar''' | ||
| Line 45: | Line 46: | ||
*Anggota pada setiap himpunan dinyatakan di dalam bentuk titik / noktah. | *Anggota pada setiap himpunan dinyatakan di dalam bentuk titik / noktah. | ||
*Apabila anggota himpunannya tidak terhingga, maka tiap – tiap anggota tidak perlu untuk dinyatakan sebagai titik. | *Apabila anggota himpunannya tidak terhingga, maka tiap – tiap anggota tidak perlu untuk dinyatakan sebagai titik. | ||
Supaya lebih jelas, perhatikan contoh di bawah ini: | Supaya lebih jelas, perhatikan contoh di bawah ini: | ||
S = {a, b, c, d, e} | S = {a, b, c, d, e} | ||
A = {b, d, e} | A = {b, d, e} | ||
Diagram venn yang sesuai dengan himpunan di atas yaitu: | Diagram venn yang sesuai dengan himpunan di atas yaitu: | ||
[[File:Diagramvenn02.jpg|center]] | |||
[[File:Diagramvenn02.jpg|thumb|center|300px]] | |||
Pada contoh diagram di atas, kalian akan mengenal istilah himpunan bagian, yakni himpunan A adalah himpunan bagian dari himpunan semesta. | Pada contoh diagram di atas, kalian akan mengenal istilah himpunan bagian, yakni himpunan A adalah himpunan bagian dari himpunan semesta. | ||
Secara matematis maka disimbolkan sebagai < | Secara matematis maka disimbolkan sebagai <math>A \subset F</math>. | ||
==Bentuk Diagram Venn== | ==Bentuk Diagram Venn== | ||
| Line 63: | Line 67: | ||
Sebagai contoh apabila ada himpunan A dan B, keduanya akan saling berpotongan jika memiliki kesamaan maka hal tersebut artinya anggota yang masuk ke dalam himpunan A masuk juga ke dalam himpunan yang B. | Sebagai contoh apabila ada himpunan A dan B, keduanya akan saling berpotongan jika memiliki kesamaan maka hal tersebut artinya anggota yang masuk ke dalam himpunan A masuk juga ke dalam himpunan yang B. | ||
Himpunan A yang berpotongan dengan himpunan B dapat ditulis dengan < | Himpunan A yang berpotongan dengan himpunan B dapat ditulis dengan <math>A \cap B </math>. | ||
===Himpunan Saling Lepas=== | ===Himpunan Saling Lepas=== | ||
Himpunan A dan B dapat disebut saling lepas apabila anggota himpunan A tidak memiliki anggota yang sama dengan anggota himpunan B. | Himpunan A dan B dapat disebut saling lepas apabila anggota himpunan A tidak memiliki anggota yang sama dengan anggota himpunan B. | ||
Himpunan yang saling lepas satu ini bisa kalian tulis dengan < | Himpunan yang saling lepas satu ini bisa kalian tulis dengan <math>A // B</math>. | ||
===Himpunan Bagian=== | ===Himpunan Bagian=== | ||
Himpunan A bisa juga disebut sebagai bagian dari himpunan B jika seluruh anggota himpunan A adalah anggota dari himpunan B. | Himpunan A bisa juga disebut sebagai bagian dari himpunan B jika seluruh anggota himpunan A adalah anggota dari himpunan B. | ||
| Line 82: | Line 86: | ||
==Hubungan Antar Himpunan== | ==Hubungan Antar Himpunan== | ||
===Irisan=== | ===Irisan=== | ||
Irisan himpunan A dan B (< | Irisan himpunan A dan B (<math>A \cap B</math>) merupakan suatu himpunan yang mana anggotanya terdapat di dalam himpunan A serta himpunan B. | ||
[[File:Diagramvenn04.jpg|center]] | |||
[[File:Diagramvenn04.jpg|thumb|center|300px]] | |||
Himpunan A ={ 0,1,2,3,4,5} serta himpunan B ={3,4,5,6,7}. | Himpunan A ={ 0,1,2,3,4,5} serta himpunan B ={3,4,5,6,7}. | ||
Perhatikanlah jika diantara kedua himpunan itu ada dua anggota yang sama yakni angka 3,4 dan 5. | Perhatikanlah jika diantara kedua himpunan itu ada dua anggota yang sama yakni angka 3,4 dan 5. | ||
Nah, dari kesamaan tersebut dapat disebut bahwa irisan himpunan A dan B dapat ditulis dengan (<code>A ∩ B</code>) = {3,4,5}. | Nah, dari kesamaan tersebut dapat disebut bahwa irisan himpunan A dan B dapat ditulis dengan (<code>A ∩ B</code>) = {3,4,5}. | ||
===Gabungan=== | ===Gabungan=== | ||
Gabungan himpunan A serta B (ditulis A | Gabungan himpunan A serta B (ditulis <math>A \cup B</math>) merupakan suatu himpunan dimana anggotanya adalah himpunan A ataupun anggota himpunan B ataupun anggota dari kedua – duanya. | ||
Gabungan antara himpunan A serta B disimbolkan dengan < | |||
[[File:Diagramvenn05.jpg|center]] | Gabungan antara himpunan A serta B disimbolkan dengan <math>A \cup B = \{x\mid x \in A </math> atau <math>x \in B \}</math> | ||
[[File:Diagramvenn05.jpg|thumb|center|300px]] | |||
Himpunan A = {1,3,5,7,9,11} serta B= {2,3,5,7,11,13}. | Himpunan A = {1,3,5,7,9,11} serta B= {2,3,5,7,11,13}. | ||
Apabila diantara himpunan A serta himpunan B digabungkan, maka akan membentuk suatu himpunan baru yang anggotanya bisa di tulis menjadi <code>A ∪ B ={1,2,3,5,7,9,11,13}</code>. | Apabila diantara himpunan A serta himpunan B digabungkan, maka akan membentuk suatu himpunan baru yang anggotanya bisa di tulis menjadi <code>A ∪ B ={1,2,3,5,7,9,11,13}</code>. | ||
===Komplemen=== | ===Komplemen=== | ||
Komplemen himpunan A (ditulis <code>Ac</code>) merupakan suatu himpunan dimana anggotanya adalah anggota himpunan semesta tetapi bukan anggota himpunan A. | Komplemen himpunan A (ditulis <code>Ac</code>) merupakan suatu himpunan dimana anggotanya adalah anggota himpunan semesta tetapi bukan anggota himpunan A. | ||
[[File:Diagramvenn06.jpg|thumb|center|300px]] | |||
S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} dan A = {1, 3, 5, 7, 9}. | S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} dan A = {1, 3, 5, 7, 9}. | ||
Bisa kalian perhatikan bahwa seluruh anggota S yang bukan dari anggota A membentuk suatu himpunan baru yakni {0,2,4,6,8}. | Bisa kalian perhatikan bahwa seluruh anggota S yang bukan dari anggota A membentuk suatu himpunan baru yakni {0,2,4,6,8}. | ||
| Line 125: | Line 132: | ||
*[[Gerbang Logika Dasar]] | *[[Gerbang Logika Dasar]] | ||
== | ==Source== | ||
*[https:// | *[https://www.yuksinau.id/diagram-venn/ yuksinaudotid] | ||
[[Category:Matematika Diskrit]] | [[Category:Matematika Diskrit]] | ||
Latest revision as of 06:55, 2 February 2023
Diagram venn merupakan suatu diagram yang menampilkan hubungan atau korelasi antar himpunan yang berkesinambungan di dalam sebuah kelompok.
Jenis diagram satu ini dicetuskan oleh seorang ilmuwan asal Inggris yang bernama John Venn.
Dengan menggunakan diagram venn ini, hubungan antar himpunan akan menjadi lebih mudah untuk dipahami.
Pada umumnya, diagram satu ini dipakai untuk menggambarkan suatu himpunan yang saling berpotongan, saling lepas dan seterusnya.
Jenis diagram ini dimanfaatkan untuk penyajian data secara saintifik serta teknik yang bermanfaat di dalam bidang matematika, statistika serta aplikasi komputer.
Himpunan
Himpunan matematika merupakan kumpulan objek yang bisa didefinisikan dengan jelas.
Sebagai contoh pakaian yang tengah kalian kenakan sekarang ini adalah sebuah himpunan, yang di dalamnya termasuk baju, topi, jaket, celana dan yang lainnya.
Kalian bisa menulis adanya sebuah himpunan dengan menggunakan tanda kurung, seperti:
{topi, baju, jaket, celana,…}
Atau kalian juga bisa menulis himpunan di dalam sebuah bilangan, seperti:
Himpunan seluruh bilangan : {0,1,2,3…}
Himpunan bilangan prima: {2,3,5,7,11,13,…}
Diagram venn yang di dalamnya berisi suatu himpunan tadi digambarkan dengan bentuk diagram sehingga mudah untuk dipahami.
Untuk cara menggambarnya, kalian dapat memperhatikan gambar di bawah ini.
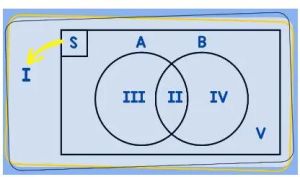
Keterangan Gambar
I. Himpunan Semesta: Menggambarkan total dari anggota yang dibicarakan.
II. Daerah yang merupakan milik himpunan A dan B (A∩B).
III. Banyak anggota himpunan A saja (tanpa B).
IV. Banyak anggota himpunan B saja (tanpa A).
V. Banyak anggota semesta tetapi bukan anggota A ataupun B.
Aturan Penggambaran Diagram Venn
Untuk membuat suatu diagram venn, maka terdapat beberapa hal yang perlu kalian perhatikan, diantaranya yaitu:
- Himpunan semesta (S) dinyatakan di dalam bentuk persegi panjang. Himpunan semesta merupakan seluruh anggota himpunan yang di dalamnya meliputi himpunan yang tengah menjadi fokus pembahasan.
- Himpunan lain yang menjadi fokus pembahasan telah dinyatakan dengan bentuk lingkaran / kurva tertutup.
- Anggota pada setiap himpunan dinyatakan di dalam bentuk titik / noktah.
- Apabila anggota himpunannya tidak terhingga, maka tiap – tiap anggota tidak perlu untuk dinyatakan sebagai titik.
Supaya lebih jelas, perhatikan contoh di bawah ini:
S = {a, b, c, d, e}
A = {b, d, e}
Diagram venn yang sesuai dengan himpunan di atas yaitu:
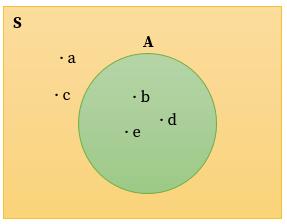
Pada contoh diagram di atas, kalian akan mengenal istilah himpunan bagian, yakni himpunan A adalah himpunan bagian dari himpunan semesta.
Secara matematis maka disimbolkan sebagai .
Bentuk Diagram Venn
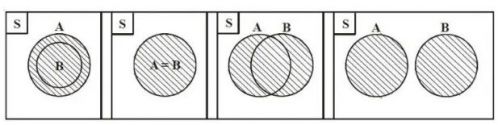
Himpunan Saling Berpotongan
Diagram satu ini digambarkan dengan dua himpunan yang saling berpotongan sebab memiliki kesamaan.
Sebagai contoh apabila ada himpunan A dan B, keduanya akan saling berpotongan jika memiliki kesamaan maka hal tersebut artinya anggota yang masuk ke dalam himpunan A masuk juga ke dalam himpunan yang B.
Himpunan A yang berpotongan dengan himpunan B dapat ditulis dengan .
Himpunan Saling Lepas
Himpunan A dan B dapat disebut saling lepas apabila anggota himpunan A tidak memiliki anggota yang sama dengan anggota himpunan B.
Himpunan yang saling lepas satu ini bisa kalian tulis dengan .
Himpunan Bagian
Himpunan A bisa juga disebut sebagai bagian dari himpunan B jika seluruh anggota himpunan A adalah anggota dari himpunan B.
Himpunan yang Sama
Diagram venn jenis menyatakan jika himpunan A serta B terdiri atas anggota himpunan yang sama, sehingga bisa kita simpulkan bahwasannya setiap anggota B adalah anggota A.
Sebagai contoh: A = {2,3,4} dan B= {4,3,2} adalah suatu himpunan yang sama sehingga kalian bisa menulisnya dengan A = B.
Himpunan yang Ekuivalen
Himpunan A dan B disebut sebagai ekuivalen jika banyaknya anggota dari kedua himpunan sama.
Himpunan A ekuivalen dengan himpunan B bisa kalian tulis dengan n(A) = n(B).
Di dalam diagram venn ada empat hubungan antar himpunan yang mencangkup irisan, gabungan, komplemen himpunan serta selisih himpunan.
Hubungan Antar Himpunan
Irisan
Irisan himpunan A dan B () merupakan suatu himpunan yang mana anggotanya terdapat di dalam himpunan A serta himpunan B.
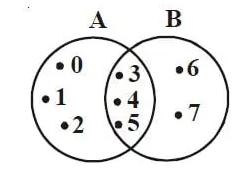
Himpunan A ={ 0,1,2,3,4,5} serta himpunan B ={3,4,5,6,7}.
Perhatikanlah jika diantara kedua himpunan itu ada dua anggota yang sama yakni angka 3,4 dan 5.
Nah, dari kesamaan tersebut dapat disebut bahwa irisan himpunan A dan B dapat ditulis dengan (A ∩ B) = {3,4,5}.
Gabungan
Gabungan himpunan A serta B (ditulis ) merupakan suatu himpunan dimana anggotanya adalah himpunan A ataupun anggota himpunan B ataupun anggota dari kedua – duanya.
Gabungan antara himpunan A serta B disimbolkan dengan atau
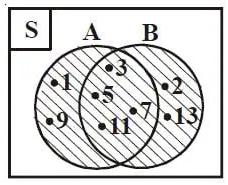
Himpunan A = {1,3,5,7,9,11} serta B= {2,3,5,7,11,13}.
Apabila diantara himpunan A serta himpunan B digabungkan, maka akan membentuk suatu himpunan baru yang anggotanya bisa di tulis menjadi A ∪ B ={1,2,3,5,7,9,11,13}.
Komplemen
Komplemen himpunan A (ditulis Ac) merupakan suatu himpunan dimana anggotanya adalah anggota himpunan semesta tetapi bukan anggota himpunan A.
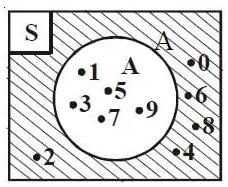
S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} dan A = {1, 3, 5, 7, 9}.
Bisa kalian perhatikan bahwa seluruh anggota S yang bukan dari anggota A membentuk suatu himpunan baru yakni {0,2,4,6,8}.
Sehingga komplemen dari himpunan A yaitu Ac = {0,2,4,6,8}.
Terkait
- Konversi Biner ke Desimal
- Konversi Desimal ke Biner
- Penjumlahan Bilangan Biner
- Pengurangan Bilangan Biner
- Equivalen
- Inferensi
- Tautologi dan Kontradiksi
- Proposisi
- Logika
- Logika Proposisi
- Varian Proposisi
- Disjungsi Inklusif dan Eksklusif
- Kuantor
- Bilangan Biner
- Bilangan Oktal
- Operasi Himpunan
- Gerbang Logika Dasar