Wiki

Bilangan Biner

Sebagai suatu sistem bilangan, bilangan biner memiliki komponen bilangan yang hanya terdiri dari dua bilangan yaitu 0 dan 1. Walaupun hanya memiliki dua buah bilangan, namun tidak membatasinya dalam melakukan berbagai operasi bilangan sebagaimana pada bilangan desimal (basis 10). Hanya saja susunannya tidak mengenal angka 2 sampai 9. Susunan bilangan biner hanya melibatkan angkan 0 dan 1. Sehingga jika dilakukan perhitungan urutannya adalah: 0, 1, 10, 11, 100, 101, 110, 111, dan seterusnya.

Jika dalam bilangan desimal dikenal dengan bilangan puluhan, ratusan, ribuan dan seterusnya, maka dalam bilangan biner tidak dikenal istilah tersebut. Yang ada dalam bilangan biner adalah kilo, mega, giga, tera dan seterusnya.

Istilah kilo hampir sama dengan 1000 dalam bilangan biner. Hanya saja ada perbedaan jumlahnya. Karena 1 kilo dalam bilangan biner tidak sama atau tepat 1000, tapi 1024. Perbedaan ini karena untuk mengambil nilai satu kilo dalam bilangan biner caranya dengan memberikan pangkat 10 dari angka 2 (bilangan biner adalah bilangan basis 2).

Selain itu juga dalam bilangan biner dikenal adanya lebar atau jumlah digit bilangan biner. Jumlah digit ini menentukan kapasitas maksimal atau besarnya bilangan yang bisa dihitung dalam bilangan biner. Misalnya saja, jika bilangan biner dengan jumlah digit 2 buah, maka bilangan maksimalnya adalah 11 (bilangan yang bisa masuk adalah: 00, 01, 10, 11). Untuk menentukan jumlah atau kapasitas maksimal bilangan biner dengan jumlah digit tertentu, bisa dilakukan dengan menggunakan perhitungan 2 pangkat jumlah digit.

Jumlah digit ini sangat berperan dalam bidang pengembangan teknologi komputasi menggunakan mesin komputasi. Untuk memahami mesin komputasi diperlukan pemahaman bilangan biner.

Bilangan biner modern ditemukan pertama kali di abad ke-17 oleh Gottfried Wilhelm Leibiz. Anda mungkin sering menjumpai gambar ilustrasi atau adegan di film-film yang berkaitan dengan dunia coding atau hacking dengan menunjukkan deretan angka 0 dan 1 yang disusun berjajar dan terdiri dari beberapa baris. Inilah yang dinamakan dengan bilangan biner.

Bilangan ini memang hanya terdiri dari dua angka saja, yakni nol (0) dan satu (1). Dalam bilangan biner digunakan pula 8 digit angka yang hanya terdiri dari angka 0 dan 1. Bilangan ini bisa dikonversikan ke dalam berbagai bentuk, mulai dari desimal, heksadesimal, ataupun oktal.

Bilangan biner berasal dari bahasa Inggris Binary. Biner atau binary bisa diartikan sebagai penulisan angka yang menggunakan dua simbol saja, yakni 0 dan 1. Sistem bilangan biner juga bisa disebut dengan istilah bit atau binary digit.

Yang menarik biner menjadi dasar dari seluruh bilangan berbasis digital. Dalam pengelompokan biner istilah komputer akan selalu berjumlah 8, dengan istilah 1 byte atau sama dengan 8 bit. Sistem semacam ini digunakan sebagai American Standard Code for Information Interchange atau disingkat ASCII.

Lalu untuk apa bilangan biner ini? Bilangan ini berfungsi untuk media komunikasi antara seluruh perangkat keras dengan komputer ataupun jaringan yang terhubung dengannya. Bisa dijabarkan bahwa angka 0 memiliki arti ‘no’, sedangkan 1 bermakna ‘yes’.

Sistem Bilangan

Ada beberapa sistem bilangan yang digunakan dalam sistem digital. Yang umum adalah sistem bilangan desimal, oktal, heksadesimal dan biner.

  • BINER (radiks / basis 2)
    • Notasi : (n)2
    • Simbol : angka 0 dan 1
  • OKTAL (radiks / basis 8)
    • Notasi : (n)8
    • Simbol : angka 0, 1, 2, 3, 4, 5, 6, 7
  • DESIMAL (radiks / basis 10)
    • Notasi : (n)10
    • Simbol : angka 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
  • HEKSADESIMAL (radiks / basis 16)
    • Notasi : (n)16
    • Simbol : angka 0,1,2,3,4,5,6,7,8,9,A,B, C,D,E,F

Sistem yang biasa digunakan dan familiar dengan kita sehari-hari adalah sistem bilangan desimal. Sistem bilangan ini bersifat alamiah karena pada kenyataannya manusia memiliki 10 jari. Bilangan desimal ini sering juga disebut basis 10. Hal ini dikarenakan perpangkatan 10 yang didapat dari 10o, 10i, 102, dst.

Sistem bilangan desimal disusun dari 10 angka atau lambang. Kesepuluh lambang tersebut adalah : 

         D = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }

Sebagai contoh dari bilangan desimal, untuk angka 978: 978(10) = (9 x 100) + (7 x 10) + (8 x 1)

Pada bilangan tersebut, digit 9 berarti 9 ratusan, 7 berarti 7 puluhan dan 8 berarti 8 satuan. Sehingga 9 memiliki arti paling besar di antara digit yang ada. Digit ini bertindak sebagai digit paling berarti (Most Significant Digit, MSD) sedangkan 8 memiliki arti yang paling kecil di antara tiga digit yang ada dan disebut sebagai digit paling tidak berarti (Least significant Digit, LSD).

Mengenal Konsep Bilangan Biner dan Desimal

Sistem bilangan biner merupakan sistem bilangan yang paling banyak digunakan dalam sistem digital karena sistem bilangan ini secara langsung dapat mewakili logika yang ada. Sistem digital hanya mengenal dua logika, yaitu 0 dan 1. Logika 0 biasanya mewakili kondisi mati dan logika 1 mewakili kondisi hidup. Pada sistem bilangan biner, hanya dikenal dua lambang, yaitu 0 dan 1. karena itu, sistem bilangan biner paling sering digunakan untuk merepresentasikan kuantitas dan mewakili keadaaan dalam sistem digital maupun sistem komputer.

Digit bilangan biner disebut binary digit atau bit. Empat bit dinamakan nibble dan delapan bit dinamakan byte. Perbedaan mendasar dari metoda biner dan desimal adalah berkenaan dengan basis. Jika desimal berbasis 10 (X10) berpangkatkan 10x, maka untuk bilangan biner berbasiskan 2 (X2) menggunakan perpangkatan 2x.

Pada sistem ini, hanya dikenal dua lambang bilangan, yaitu : 

         B = { 0, 1 }

Ciri suatu bilangan biner adalah adanya tambahan subskrip bin atau 2 atau tambahan huruf B di akhir bilangan. Contoh : 1010011bin = 10100112 = 1010011B.

  • Untuk Desimal
14(10) = (1 x 101) + (4 x 100)
= 10 + 4 = 14
  • Untuk Biner
1110(2) = (1 x 23) + (1 x 22) + (1 x 21) + (0 x 20)
= 8 + 4 + 2 + 0 = 14

Menghitung Bilangan Biner

Ada banyak cara untuk menghitung bilangan biner. Sehingga bisa menyesuaikan dengan keinginan atau kebutuhan. Misalnya jika ingin mengkonversi bilangan biner ke desimal, maka ada teknik atau perhitungan khusus yang perlu dilakukan.

Salah satunya dengan memasukkan sederet angka biner tersebut ke masing-masing bagian bilangan biner. Sebelumnya perlu Anda ketahui bahwa untuk mengubah bilangan biner ke desimal maka kita perlu menulis nilai dari masing-masing angka biner seperti berikut.

 

Selanjutnya masukkan bilangan biner ke dalam masing-masing kolom tersebut. Misalnya kita akan mengkonversi 00001010 ke dalam desimal. Maka caranya bisa Anda lihat pada gambar di bawah ini.

 

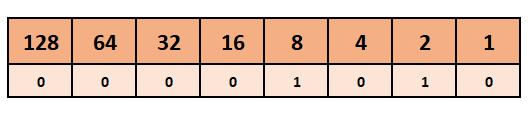
Dari tabel tersebut kita hanya perlu menghitung atau menjumlahkan angka-angka yang memiliki nilai 1. Berdasarkan contoh di atas dapat kita ketahui bahwa konversi bilangan biner tersebut adalah 8 + 2 = 10. Dengan cara di atas Anda bisa melakukan konversi biner ke desimal dengan lebih mudah dan cepat.

Character Binary Code Character Binary Code
A 01000001 a 01100001
B 01000010 b 01100010
C 01000011 c 01100011
D 01000100 d 01100100
E 01000101 e 01100101
F 01000110 f 01100110
G 01000111 g 01100111
H 01001000 h 01101000
I 01001001 i 01101001
J 01001010 j 01101010
K 01001011 k 01101011
L 01001100 l 01101100
M 01001101 m 01101101
N 01001110 n 01101110
O 01001111 o 01101111
P 01010000 p 01110000
Q 01010001 q 01110001
R 01010010 r 01110010
S 01010011 s 01110011
T 01010100 t 01110100
U 01010101 u 01110101
V 01010110 v 01110110
W 01010111 w 01110111
X 01011000 x 01111000
Y 01011001 y 01111001
Z 01011010 z 01111010

Terkait

Source

Retrieved from "https://kangtain.com/wiki/index.php?title=Bilangan_Biner&oldid=8421"