Operasi Himpunan: Difference between revisions
| (4 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
Objek atau elemen himpunan ditulis dengan menggunakan sepasang kurung kurawal <code>{ . . . }</code> | Objek atau elemen himpunan ditulis dengan menggunakan sepasang kurung kurawal <code>{ . . . }</code> | ||
B = {1,3,5} | B = {1,3,5} | ||
A = {a,b,c,d} | A = {a,b,c,d} | ||
| Line 37: | Line 36: | ||
===Gabungan=== | ===Gabungan=== | ||
A gabungan B ditulis menjadi : | A gabungan B ditulis menjadi : | ||
A ∪ B = {x | x ∈ A atau x ∈ B} | A ∪ B = {x | x ∈ A atau x ∈ B} | ||
*'''Contoh''' | |||
A = {1, 2, 3, 4, 5} | A = {1, 2, 3, 4, 5} | ||
| Line 54: | Line 54: | ||
A – B = { x | x ∈ A dan x ∉ B } | A – B = { x | x ∈ A dan x ∉ B } | ||
*'''Contoh''' | |||
A = {1, 2, 3, 4, 5} | A = {1, 2, 3, 4, 5} | ||
B = {2, 3, 5, 7, 11} | B = {2, 3, 5, 7, 11} | ||
Latest revision as of 18:40, 15 November 2021
Himpunan adalah kumpulan benda atau objek yang dapat didefinisikan dengan jelas.
Benda atau objek dalam himpunan disebut elemen atau anggota himpunan.
Objek atau elemen himpunan ditulis dengan menggunakan sepasang kurung kurawal { . . . }
B = {1,3,5}
A = {a,b,c,d}
R = { a, b, {a, b, c}, {a, c} }
Penyajian
Terdapat 4 cara untuk menyajikan himpunan, yaitu mengenumerasikan elemen-elemen nya, menggunakan simbol-simbol baku menyatakan syarat keanggotaan menggunakan diagram venn.
Jenis – jenis Himpunan
- Himpunan Bagian (Subset)
- Himpunan Kosong (Nullset)
- Himpunan Semesta
- Himpunan Sama (Equal)
- Himpunan Lepas
- Himpunan Ekuivalen ( Equal Set )
- Himpunan Komplemen ( Complement Set )
Operasi Himpunan
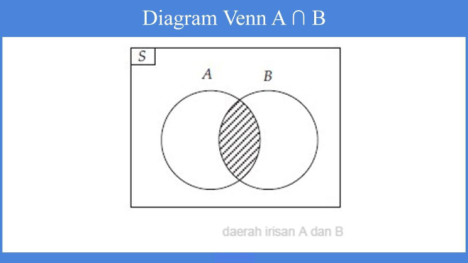
Irisan
Irisan dari dua himpunan A dan B merupakan himpunan yang di mana setiap anggotanya terdapat di himpunan A dan juga terdapat di dalam himpunan B. atau himpunan yang anggotanya terdapat di kedua himpunan tersebut.
A = {a, b, c, d, e} dan B = {b, c, f, g, h}
Pada kedua himpunan di atas terdapat dua anggota yang sama yakni b dan c. Oleh sebab itu, bisa dinyatakan bahwa irisan himpunan A dan B merupakan b dan c atau ditulis dengan:
A ∩ B = {b, c}
A ∩ B dibaca: himpunan A irisan himpunan B. Dengan diagram Venn A ∩ B juga bisa dinyatakan seperti pada gambar di bawah ini:
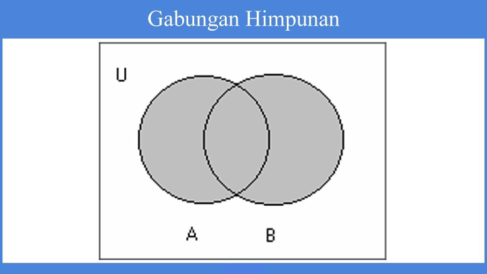
Gabungan
A gabungan B ditulis menjadi :
A ∪ B = {x | x ∈ A atau x ∈ B}
- Contoh
A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
A ∪ B = {1, 2, 3, 4, 5, 7, 11}
Apabila dinyatakan dalam bentuk diagram Venn maka:
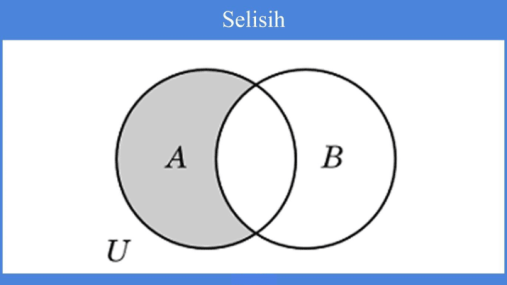
Selisih
A Selisih B ditulis menjadi:
A – B = { x | x ∈ A dan x ∉ B }
- Contoh
A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
A-B = {1, 4}
Apabila dinyatakan dalam bentuk diagram Venn maka: