Sistem Digital:Desain Digital dengan Karnough Map: Difference between revisions
Created page with "==Konsep Penyederhanaan Desain Digital== Tahap minimalisasi rangkaian logika diperlukan agar diperoleh rangkaian dengan fungsi yang sama namun menggunakan gerbang yang paling sedikit. Rangkaian dengan jumlah gerbang yang paling sedikit akan lebih murah harganya, dan dari segi tata letak komponennya akan lebih sederhana. Selain harga murah konsumsi daya yang diperlukan juga rendah sehingga sistem dapat bekerja lebih cepat. ==Karnough Map== Peta Karnaugh digunakan sebag..." |
m Kangtain moved page Materi/Sistem Digital/Desain Digital dengan Karnough Map to Sistem Digital:Desain Digital dengan Karnough Map |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
Cara penyederhanaan dapat dilakukan dengan Aljabar Boole dan Peta Karnaugh (K-Maps). | Cara penyederhanaan dapat dilakukan dengan Aljabar Boole dan Peta Karnaugh (K-Maps). | ||
[[File:Karnough Map 2.png|thumb|center|300px]] | |||
==Karnough Map untuk 3 Variabel== | |||
[[File:Karnough Map 9.png|thumb|center|300px]] | |||
Perhatikan: Nilai “11” tidak berada di kolom paling kanan. | |||
[[File:Karnough Map 10.png|thumb|center|300px]] | |||
Memetakan tabel kebenaran dalam kotak segi empat yang jumlahnya tergantung jumlah variabel masukan | |||
Penyederhanaan untuk setiap “1” yang bersebelahan menjadi suku minterm sederhana. | |||
Aljabar Boole sbb: | |||
1. ABC’ + ABC = AB(C’ + C) = AB | |||
2. A’B’C + A’BC + ABC + AB’C = A’C(B’ + B) + AC(B + B’) | |||
A’C + AC = C(A’ + A) = C | |||
Hasil Akhir : AB + C | |||
==Desain Digital 3 Variabel== | |||
Memetakan tabel kebenaran dalam kotak segi empat yang jumlahnya tergantung jumlah variabel masukan. | |||
<code>A</code> = sensor Infra Red, <code>B</code> = sensor berat, <code>C</code> = sensor ultrasonic. | |||
Penyederhanaan untuk setiap output “1” yang bersebelahan menjadi suku minterm sederhana. | |||
[[File:Karnough Map 11.png|thumb|center|300px]] | |||
Aljabar Boole sbb: | |||
1. A’BC’ + ABC’ + A’BC + ABC | |||
BC’(A’ + A) + BC(A’ + A) = BC’ + BC = B(C’ + C) = B | |||
2. ABC’ + AB’C’ = AC’(B + B’) = AC’ | |||
Hasil Akhir : B + AC’ | |||
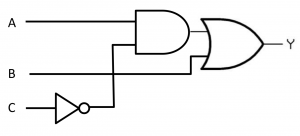
Hasil Akhir : Y = B + AC’ | |||
[[File:Karnough Map 12.png|thumb|center]] | |||
__NOINDEX__ | |||
Latest revision as of 22:33, 19 November 2022
Konsep Penyederhanaan Desain Digital
Tahap minimalisasi rangkaian logika diperlukan agar diperoleh rangkaian dengan fungsi yang sama namun menggunakan gerbang yang paling sedikit.
Rangkaian dengan jumlah gerbang yang paling sedikit akan lebih murah harganya, dan dari segi tata letak komponennya akan lebih sederhana.
Selain harga murah konsumsi daya yang diperlukan juga rendah sehingga sistem dapat bekerja lebih cepat.
Karnough Map
Peta Karnaugh digunakan sebagai cara untuk menyederhanakan persamaan logika secara grafis, atau dapat pula dipandang sebagai metoda untuk mengubah suatu tabel kebenaran ke rangkaian logika yang sesuai secara sederhana dan rapi.
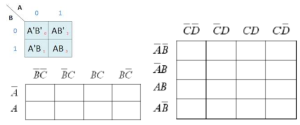
Cara penyederhanaan dapat dilakukan dengan Aljabar Boole dan Peta Karnaugh (K-Maps).
Karnough Map untuk 3 Variabel
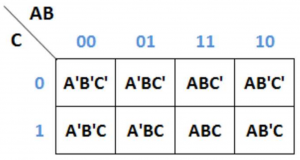
Perhatikan: Nilai “11” tidak berada di kolom paling kanan.
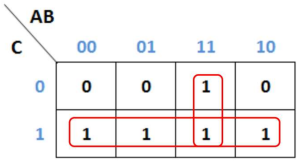
Memetakan tabel kebenaran dalam kotak segi empat yang jumlahnya tergantung jumlah variabel masukan
Penyederhanaan untuk setiap “1” yang bersebelahan menjadi suku minterm sederhana.
Aljabar Boole sbb:
1. ABC’ + ABC = AB(C’ + C) = AB 2. A’B’C + A’BC + ABC + AB’C = A’C(B’ + B) + AC(B + B’) A’C + AC = C(A’ + A) = C Hasil Akhir : AB + C
Desain Digital 3 Variabel
Memetakan tabel kebenaran dalam kotak segi empat yang jumlahnya tergantung jumlah variabel masukan.
A = sensor Infra Red, B = sensor berat, C = sensor ultrasonic.
Penyederhanaan untuk setiap output “1” yang bersebelahan menjadi suku minterm sederhana.
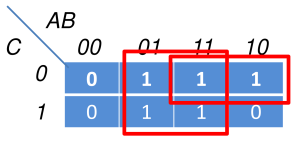
Aljabar Boole sbb:
1. A’BC’ + ABC’ + A’BC + ABC BC’(A’ + A) + BC(A’ + A) = BC’ + BC = B(C’ + C) = B 2. ABC’ + AB’C’ = AC’(B + B’) = AC’ Hasil Akhir : B + AC’
Hasil Akhir : Y = B + AC’