Sistem Digital:Aljabar Boolean
Aljabar Boolean (Tahun 1849)
Boole memberikan skema untuk deskripsi aljabar dari proses berpikir secara logika
Deskripsi aljabar digunakan untuk menjabarkan rangkaian Sistem Digital
Menyederhanakan suatu ekspresi Sistem Digital untuk implementasi fisik rangkaian yang lebih sederhana
Aljabar Boolean adalah salah satu model yang digunakan dalam proses analisis yang diperlukan untuk mendeskripsikan fungsi logika rangkaian Sistem Digital.
Sistem Digital dapat dinyatakan dalam deskripsi tekstual, tabel kebenaran.
Rangkaian logika bisa diperoleh dari persamaan logika yang telah disederhanakan
Penyederhanaan persamaan logika dilakukan menggunakan aljabar Boolean.
Implementasi fungsi logika menjadi suatu rangkaian logika baik menggunakan tabel kebenaran maupun aljabar Boolean, sebagai berikut:
- Penyederhanaan persamaan secara aljabar
- Ekspresi logika dari tabel kebenaran
- Analisis Minterm, persamaan SOP (Sum of Product) dan notasi kanonik SOP
- Analisis Maxterm, persamaan POS (Product of Sum) dan notasi kanonik POS
- Konversi SOP ke POS dan sebaliknya
Pembahasan Aljabar Boolean
Aljabar Boolean menggunakan aturan-aturan yang diturunkan dari asumsi dasar (aksioma/dalil/postulat), sebagai berikut:
0 · 0 = 0
1 · 1 = 1
0 · 1 = 1 · 0 = 0
Jika x = 0, maka x = 1
1 + 1 = 1
0 + 0 = 0
1 + 0 = 0 + 1 = 1
Jika x = 1, maka x = 0
Pembahasan Hukum-hukum Aljabar
Hukum-hukum Aljabar mendefinisikan aturan untuk persamaan dengan banyak variabel, sebagai berikut:

Hukum-hukum Aljabar mendefinisikan aturan untuk persamaan dengan banyak variabel, sebagai berikut:

Analisis Rangkaian Sistem Digital Jika dalam satu ekspresi tidak terdapat tutup kurung, maka operasi fungsi logika dilakukan dengan urutan:
- NOT
- AND
- OR
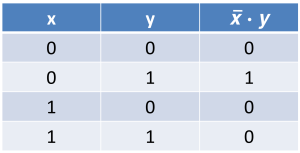
Analisis Rangkaian Sistem Digital
Misalnya ekspresi
- variabel
xdi inversikan, kemudian di-AND- kan dengan variabely