Sistem Digital:Karnough Map: Difference between revisions
No edit summary |
|||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:Karnough Map 1.png|thumb]] | [[File:Karnough Map 1.png|thumb|318x318px]] | ||
Karnaugh Map atau K-Map adalah suatu teknik penyederhanaan fungsi logika dengan cara pemetaan. | Karnaugh Map atau K-Map adalah suatu teknik penyederhanaan fungsi logika dengan cara pemetaan. | ||
| Line 26: | Line 26: | ||
==Penyajian Kmap 2-variabel== | ==Penyajian Kmap 2-variabel== | ||
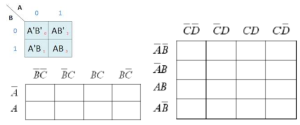
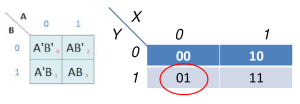
Pada penyajian Kmap 2-variabel dibutuhkan 4 (2 n ) kotak persegi untuk Kmap. Cara mengisi masing-masing kotak persegi pada Kmap ditunjukkan pada gambar. | Pada penyajian Kmap 2-variabel dibutuhkan 4 (2<sup>n</sup>) kotak persegi untuk Kmap. Cara mengisi masing-masing kotak persegi pada Kmap ditunjukkan pada gambar. | ||
Terdapat berbagai macam cara dalam menyusun matriks Kmap dan kita boleh memilih, dengan syarat tetap konsisten pada posisi dimana minterm berada. | Terdapat berbagai macam cara dalam menyusun matriks Kmap dan kita boleh memilih, dengan syarat tetap konsisten pada posisi dimana minterm berada. | ||
| Line 37: | Line 37: | ||
[[File:Karnough Map 4.png|thumb|center]] | [[File:Karnough Map 4.png|thumb|center]] | ||
Pada penyajian Kmap 2-variabel dibutuhkan 4 (2 n ) kotak persegi untuk Kmap. | Pada penyajian Kmap 2-variabel dibutuhkan <code>4 (2<sup>n</sup>)</code> kotak persegi untuk Kmap. | ||
[[File:Karnough Map 5.png|thumb|center]] | |||
maka ekspresi [[File:Karnough Map 6.png|90px]] | |||
[[File:Karnough Map 7.png|thumb|center]] | |||
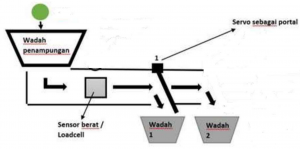
==Rangkaian Sortir Berat== | |||
[[File:Karnough Map 8.png|thumb|center]] | |||
[[Category:Materi]] | |||
[[Category:Matkul]] | |||
[[Category:Sistem Digital]] | |||
Latest revision as of 21:52, 30 November 2022

Karnaugh Map atau K-Map adalah suatu teknik penyederhanaan fungsi logika dengan cara pemetaan.
K-Map terdiri dari kotak-kotak yang jumlahnya terdiri dari jumlah variable.
Penyederhanaan fungsi logika dengan cara pemetaan berdasarkan fungsi logika atau jumlah inputan dari rangkaian logika.
Karnough Map (Kmap) adalah diagram yang merepresentasikan table kebenaran menggunakan matriks kotak persegi (cells).
Setiap kotak persegi (cells) mewakili nilai minterm (maxterm) dari logic function.
Kmap membantu menyederhanakan persamaan dari table kebenaran untuk rangkaian yang kompleks.
Kmap memiliki beberapa kelebihan, diantaranya adalah lebih sederhana dalam proses penyederhanaannya untuk memperoleh jumlah gerbang yang lebih sedikit.
Apabila ada fungsi n-variabel, dibutuhkan 2 n baris table kebenaran, dan pada Kmap dibutuhkan 2 n kotak persegi.
Nilai dari table kebenaran tersebut ditulis kembali di kotak persegi pada posisi yang mewakli posisinya di table kebenaran.
Langkah-langkah menyajikan fungsi ke dalam Kmap adalah :
- Buat diagram matriks sebanyak
2nkotak persegi, dimananadalah jumlah variable fungsi. - Setiap kotak-kotak persegi tersebut diisi sesuai dengan nilai yang diberikan dari fungsi atau nilai dari table kebenaran pada letak yang tepat.
Penyajian Kmap 2-variabel
Pada penyajian Kmap 2-variabel dibutuhkan 4 (2n) kotak persegi untuk Kmap. Cara mengisi masing-masing kotak persegi pada Kmap ditunjukkan pada gambar.
Terdapat berbagai macam cara dalam menyusun matriks Kmap dan kita boleh memilih, dengan syarat tetap konsisten pada posisi dimana minterm berada.
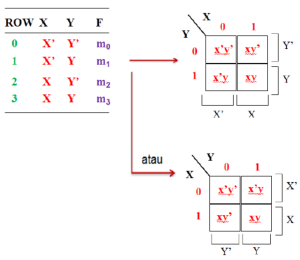
Analisis Karnough Map Rangkaian Sistem Digital
Pada penyajian Kmap 2-variabel dibutuhkan 4 (2n) kotak persegi untuk Kmap.
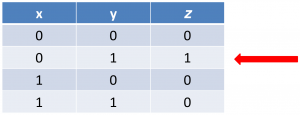
Pada penyajian Kmap 2-variabel dibutuhkan 4 (2n) kotak persegi untuk Kmap.
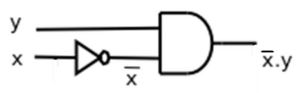
Rangkaian Sortir Berat